昨天在科学网上得知这样一个新闻《越南小学数学题难倒博士》,据悉题目来自越南保禄小学三年班,不过报道称该题难倒了上至博士下至家长,未免也太言过其实了。
题目描述
学生需要在下图表格中按由上至下、从左到右的顺序,填入1~9的数字,可重复填写,并按先乘除后加减(图中冒号代表除法)的运算法则,完成整条算式。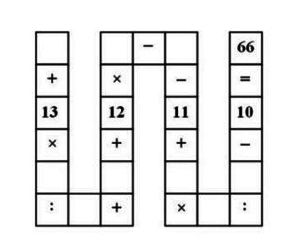
解题方法
显然,这题对于我们这种程序员来说完全不是问题,只要在大一上过C语言的学生(我们学校全校都学过C,即使是文科专业)基本上都可以用九重for循环来穷举解出此题,下面我分别用C和Matlab实现,并对Matlab算法进行了改进。
C语言实现:
1 |
|
结果显示如下: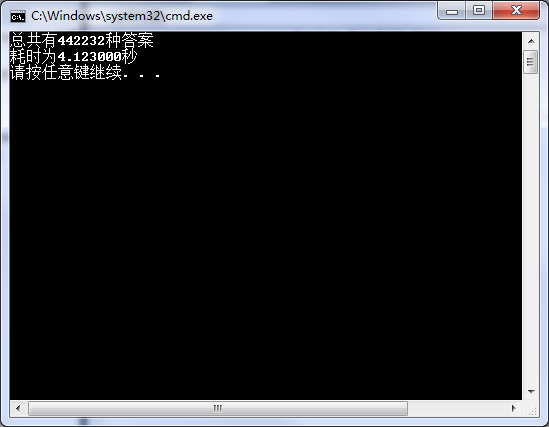
Matlab实现
- 最直接的方法:耗时4911.131591 秒。
1 | clear all;ans=[]; |
在上面的算法中,存储结果answer的操作十分耗时,我们可以想办法来优化。于是,我将存储结果的过程注释掉后(去掉if语句块),耗时为16.814298 秒,时间由一个小时缩短到了十几秒。不过即使不储存结果,也耗时16.814298 秒,这与用C语言(同样也没有存储结果)的4秒还是有差距的!下面我来讲讲如何改进算法。
改进的matlab实现
在之前的文章《Matlab高效编程技巧》中,提到了要尽量避免多重循环,多使用向量化函数。因此,我决定用矩阵来代替这$9$重循环。
首先从简单的例子出发:假设有$2$个一维数组$a,b$,其元素都是$1:9$,显然这$2$个数组任意元素之间进行四则运算(在这里我们假设是相乘)的结果有$9\times 9$项,可以用一个$9\times 9$的二维数组表示;同理,假设有$3$个一维数组$a,b,c$,其元素都是$1:9$,我们要计算这三个数组任意元素之间进行四则运算的结果,这样总共有$9\times 9\times 9$项,正好用一个$9\times 9\times 9$的三维数组存储;依此类推,我们可以得到$9$个一维数组元素间进行四则运算可以用$9\times 9\times 9\times 9\times 9\times 9\times 9\times 9\times 9\times 9$的$9$维数组表示。
然而,在matlab中,乘法符号只能用于二维数组的相乘,幸好我们可以通过bsxfun函数来进行不同维数数组的计算.下面举例演示一下bsxfun的用法:
1 | clear all |
通过运行上述结果,你就可以发现,bsxfun完成了任意元素间两两进行四则运算的结果,而且并不要求维数相等。当然关于bsxfun的运算原理以及作用可以查看Matlab的自带文档。我们的算法只需要上述的功能就可以了,在程序中,我按照公式$a+13\cdot b/c+d+12\cdot e-f-11+g\cdot h/i-10$计算了当$a, b, \cdots, i$的所有组合的值,并存储在abcdefghi中,最后再找到数组abcdefghi中值为66的元素所在的下标索引,其索引就是问题的解。具体的Matlab程序实现如下:
1 | clear all |
运行结果如下图: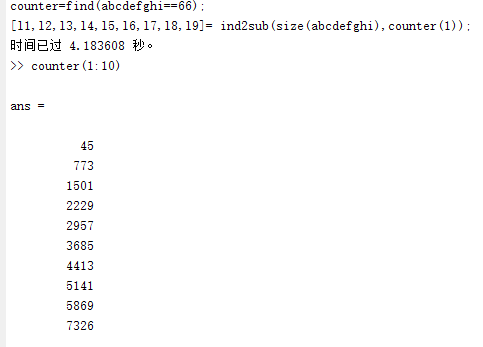
从图中可以看到,此方法耗时4.183608秒,图中我只显示了前十个结果,并且只计算了第一个结果45所对应的abcdefghi的值,其值在下图的变量空间中: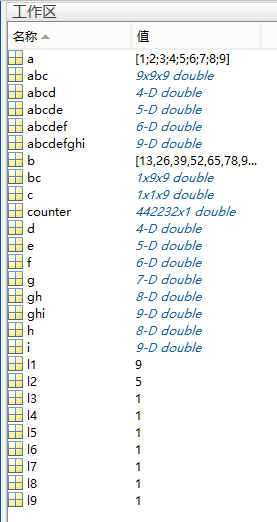
从上图中可以看出,counter大小为442232,即总共有442232个解,其中counter(1)=45时,对应的解为abcdefghi=9 5 1 1 1 1 1 1 1 1 1。
注释:此程序在内存较小的电脑中会由于内存不够而运行不成功,我是在实验室的工作站(内存128g)上运行的。
结果分析
使用matlab编程时,要避免使用多重循环,尽量以矩阵的角度思考问题。由上面的程序耗时对比可以看出,用C语言实现和我改进的算法耗时都在4秒左右,而且用C语言实现是在没有存储解的结果的情况下,如果同样的要存储结果(存储结果可以用不同的数据结构:链表、队列等等)的话,谁更耗时还说不定!由文中提到的两种matlab实现可知,第一种方法占用内存小,可以在普通的电脑上运行,但是耗时长;而我们改进的算法,耗时短,但是占用内存大,在内存小的机器上无法运行。这就是所谓的时间换空间,空间换时间吧!

